MECÂNICA GRACELI GENER. - QUÂNTICA DIMENSIONAL TENSORIAL RELATIVISTA DE CAMPOS [714]

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

[

$\psi ^{*}$

$TeoriaInteraçãomediadorMagnitude relativaComportamentoFaixaCromodinâmicaForça nuclear forteGlúon10411/r71,4 × 10-15 mEletrodinâmicaForça eletromagnéticaFóton10391/r2infinitoFlavordinâmicaForça nuclear fracaBósons W e Z10291/r5 até 1/r710-18 mGeometrodinâmicaForça gravitacionalgráviton101/r2infinito$

Teoria	Interação	mediador	Magnitude relativa	Comportamento	Faixa
Cromodinâmica	Força nuclear forte	Glúon	1041	1/r7	1,4 × 10-15 m
Eletrodinâmica	Força eletromagnética	Fóton	1039	1/r2	infinito
Flavordinâmica	Força nuclear fraca	Bósons W e Z	1029	1/r5 até 1/r7	10-18 m
Geometrodinâmica	Força gravitacional	gráviton	10	1/r2	infinito

$G* = OPERADOR DE DIMENSÕES DE GRACELI.$

DIMENSÕES DE GRACELI SÃO TODA FORMA DE TENSORES, ESTRUTURAS, ENERGIAS, ACOPLAMENTOS, , INTERAÇÕES E CAMPOS, DISTRIBUIÇÕES ELETRÔNICAS, ESTADOS FÍSICOS, ESTADOS QUÂNTICOS, ESTADOS FÍSICOS DE ENERGIAS DE GRACELI, E OUTROS.

A lei de Faraday-Neumann-Lenz,^{[nota 1]} ou lei da indução de Faraday, ou simplesmente, lei da indução eletromagnética, é uma das equações básicas do eletromagnetismo. Ela prevê como um campo magnético interage com um circuito elétrico para produzir uma força eletromotriz — um fenômeno chamado de indução eletromagnética. É a base do funcionamento de transformadores, alternadores, dínamos, indutores, e muitos tipos de motores elétricos, geradores e solenoides.^[1]^[2]

Atribui-se a Michael Faraday a descoberta da indução eletromagnética e, por conseguinte, o nome da lei relativa a esse fenômeno. Este foi comprovado experimentalmente por Faraday diversas vezes, apesar de sua explicação limitar-se ao conceito de linhas de força. A primeira formulação matemática da lei de Faraday foi feita por Franz Ernst Neumann em 1845. Nela, a força eletromotriz produzida em um circuito, pela indução, era expressa pelo negativo da derivada do fluxo magnético com o tempo através da área delimitada por esse circuito. O sinal negativo diz respeito ao sentido da FEM – e, por conseguinte, da corrente elétrica – e pode ser expressa formalmente por meio da chamada Lei de Lenz, desenvolvida por Heinrich Lenz em 1834, que integra o corolário da lei de Faraday.

Suas aplicações são inúmeras; na prática, quase todos os equipamentos eletro-eletrônicos utilizam o fenômeno da indução, seja para produzir uma corrente contínua, como nos dínamos, ou uma corrente alternada, como nos geradores, transformadores, alternadores e indutores, todos por meio da variação no campo magnético.

A equação de Maxwell–Faraday é uma generalização da lei de Faraday, e compõe uma das equações de Maxwell. Ela descreve como a variação de um campo magnético no tempo através de um circuito em repouso produz um campo elétrico não-eletrostático que, por sua vez, produz uma corrente elétrica no circuito. O movimento relativo entre um imã e o condutor e a produção, ou não, de um campo elétrico nessa experiência levaram a uma aparente dicotomia, exercendo, por sua vez, papel fundamental no desenvolvimento da relatividade restrita por Albert Einstein em 1905.

História

A indução eletromagnética foi descoberta de forma independente por Michael Faraday em 1831 e Joseph Henry em 1832.^[3] Faraday, no entanto, foi o primeiro a publicar os resultados de seus experimentos.^[4] Em 29 de agosto de 1831, data da primeira demonstração experimental da indução eletromagnética feita por Faraday,^[5] ele amarrou dois fios em lados opostos de um anel de ferro (ou toro, um arranjo similar a um transformador toroidal moderno). Face às recém-descobertas propriedades do eletromagnetismo, ele esperava que, quando a corrente começasse a passar em um fio, uma espécie de onda viajaria através do anel e causaria algum efeito elétrico no lado oposto. Conectou, então, um dos fios a um galvanômetro e o outro a uma bateria. Foi observada, de fato, uma corrente transiente – que ele chamou de "onda de eletricidade" – nos momentos em que conectou e desconectou o fio à bateria.^[6] Esta indução ocorreu devido à mudança que houve no fluxo magnético quando a bateria foi conectada e desconectada.^[7]

Ilustração do aparato usado por Faraday em sua primeira demonstração da indução eletromagnética.

Faraday explicou a indução eletromagnética usando um conceito que chamou de linhas de força. No entanto, grande parte dos cientistas da época rejeitavam suas ideias teóricas, principalmente porque não havia uma formulação matemática para elas.^[8] James Clerk Maxwell, contudo, usou as ideias de Faraday como a base para sua teoria eletromagnética quantitativa.^[8]^[9] Nos estudos de Maxwell, o aspecto da variabilidade com o tempo da indução eletromagnética é expressado como uma equação diferencial, a qual Oliver Heaviside referiu-se como a lei de Faraday, embora seja diferente da versão original da lei de Faraday. A versão de Heaviside é a forma que hoje é reconhecida como parte do grupo de equações conhecido como equações de Maxwell.

A lei de Lenz, formulada por Heinrich Lenz em 1834, descreve o "fluxo através do circuito", e fornece a direção da força eletromotriz e corrente induzidas resultantes da indução eletromagnética.

Lei de Faraday-Neumann-Lenz

Enunciado qualitativo

A versão mais difundida da lei de Faraday afirma:

A força eletromotriz induzida em qualquer circuito fechado é igual ao negativo da variação do fluxo magnético com o tempo na área delimitada pelo circuito.^[10]^[11]

Esta versão da lei de Faraday é estritamente válida apenas quando o circuito fechado é um laço de fio metálico infinitamente fino,^[12] e é inválida em outras circunstâncias a serem discutidas. Uma versão diferente, a equação de Maxwell–Faraday, é válida em todas as circunstâncias.

Enunciado quantitativo

A lei da indução de Faraday faz uso do fluxo magnético Φ_B através de uma superfície hipotética Σ, cujo bordo é um laço de fio metálico. Uma vez que o laço pode estar se movendo com o tempo, escreve-se Σ(t) para a superfície. O fluxo magnético é definido pela integral de superfície:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\Phi _{B}=\iint \limits _{\Sigma (t)}{\mathbf {B} }({\mathbf {r} },t)\cdot d{\mathbf {A} }\

onde dA é um elemento de área da superfície Σ(t), B é o campo magnético (também chamado de "densidade do fluxo magnético"), e B·dA é um produto escalar dos dois vetores (a quantidade infinitesimal de fluxo magnético). De outro modo, o fluxo magnético através do laço é proporcional ao número de linhas do fluxo magnético que passam por ele.

Quando o fluxo se modifica — devido a uma mudança do B, ou porque o laço é movido ou deformado, ou ambos — a lei da indução de Faraday afirma que o fio adquire uma FEM, ε, definida como o trabalho por unidade de carga que uma força não-eletrostática realiza quando uma carga é transportada em volta do laço.^[12]^[13]^[14]^{[nota 2]} De forma equivalente, é a voltagem que seria medida ao cortar o arame para criar um circuito aberto, ligando um voltímetro às pontas.

A lei de Faraday afirma que a FEM também é dada pela taxa de variação do fluxo magnético:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {E}}=-{{d\Phi _{B}} \over dt}\

onde ε é a força eletromotriz (FEM) e Φ_B é o fluxo magnético. A direção da FEM é dada pela lei de Lenz.

Para um fio enrolado firmemente em uma bobina, composta de N voltas idênticas, cada uma com o mesmo Φ_B, a lei da indução de Faraday afirma:^[15]^[16]

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

{\mathcal {E}}=-N{{d\Phi _{B}} \over dt}

onde N é o número de voltas do fio e Φ_B é o fluxo magnético através de uma única volta.

Equação de Maxwell-Faraday

A equação de Maxwell-Faraday é uma generalização da lei de Faraday, e afirma que um campo magnético que varia com o tempo é sempre acompanhado por um campo elétrico não-conservativo que varia espacialmente, e vice-versa. A equação de Maxwell–Faraday é:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\nabla \times {\mathbf {E} }=-{\frac {\partial {\mathbf {B} }}{\partial t}}

(em unidades do SI), onde $\nabla \times$ é o operador rotacional e, novamente, E(r, t) é o campo elétrico e B(r, t) é o campo magnético. Tais campos podem estar em função da posição r e do tempo t.

A equação de Maxwell–Faraday é uma das quatro equações de Maxwell, tendo, portanto, um papel fundamental na teoria do eletromagnetismo clássico. Ela também pode ser escrita na forma integral pelo Teorema de Kelvin-Stokes:^[17]

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

$\oint _{\partial \Sigma }{\mathbf {E} }\cdot d{\boldsymbol {\ell }}=-\iint _{\Sigma }{\frac {\partial {\mathbf {B} }}{\partial t}}\cdot d{\mathbf {A} }$ ,

onde Σ é uma superfície limitada pelo seu bordo ∂Σ; E é o campo elétrico; B é o campo magnético; dℓ é um elemento vetorial infinitesimal de ∂Σ; dA é um elemento vetorial infinitesimal de Σ.

Ambos dℓ e dA têm uma ambiguidade de sinal; para obter o sinal correto, usa-se a regra da mão direita. Para uma superfície plana Σ, um elemento de curva positivo dℓ da curva ∂Σ é definido pela regra de mão direita como estando na direção dos dedos da mão direita quando o polegar aponta na direção do vetor normal n exterior à superfície Σ.

A lei de Gauss é a lei que estabelece a relação entre o fluxo do campo elétrico através de uma superfície fechada com a carga elétrica que existe dentro do volume limitado por esta superfície. A lei de Gauss é uma das quatro equações de Maxwell, juntamente com a lei de Gauss do magnetismo, a lei da indução de Faraday e a lei de Ampère-Maxwell. Foi elaborada por Carl Friedrich Gauss em 1835, porém só foi publicada após 1867.^[1] Gauss foi um matemático alemão que fez contribuições importantes para a teoria dos números, a geometria e a probabilidade, tendo também contribuições em astronomia e na medição do tamanho e do formato da Terra.^[2]

Fluxo do campo elétrico

Linhas de campo elétrico "furando" uma superfície, mostrando que o existe fluxo de campo elétrico através da superfície. Como as linhas de campo estão saindo da superfície, o fluxo do campo elétrico é positivo.

O fluxo de campo elétrico, $\Phi _{E}$ , é uma grandeza escalar e pode ser considerado como uma medida do número de linhas de campo que atravessam a superfície.^[2]^[3] Convenciona-se que se há mais linhas de campo saindo da superfície do que entrando, o fluxo do campo elétrico através da superfície é positivo e se há mais linhas de campo entrando na superfície do que saindo da mesma, o fluxo é negativo. Além disso, é importante observar o fato de que se o número de linhas de campo que entra na superfície é igual ao número de linhas de campo que sai da superfície, então o fluxo de campo elétrico através da superfície é nulo.^[2]^[4]

Para obter o fluxo do campo elétrico E através de uma superfície fechada em que E é não-uniforme, é preciso dividi-la em elementos de área infinitesimal dA. Define-se, então, um vetor dA cujo módulo é dA, a direção é perpendicular ao elemento de área e o sentido é adotado como o sentido da normal ao elemento infinitesimal saindo da superfície. Assim, esses elementos infinitesimais são tão pequenos que E pode ser considerado constante em todos os pontos de um mesmo elemento de área.^[2] Portanto, podemos definir o fluxo de E através de uma superfície S da seguinte forma:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\Phi _{E}=\int _{S}\mathbf {E} \cdot \mathrm {d} \mathbf {A}

ou, no caso de uma superfície fechada:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

$\Phi _{E}=\oint _{S}\mathbf {E} \cdot \mathrm {d} \mathbf {A} \,\!$

Da definição de produto escalar, tem-se que: E . dA = |E||dA| cosθ = |E|cosθ |dA|. Como θ é o ângulo entre os vetores E e dA, |E|cosθ é a projeção do vetor E sobre o vetor dA, logo a função desse produto escalar dentro da integral é selecionar algo proporcional à componente do campo elétrico que está "furando" à superfície infinitesimal dA, o que é coerente com a definição de fluxo dada anteriormente.

Por fim, se uma carga pontual estiver fora da superfície, as linhas de campo que partem da carga pontual irão entrar e sair da superfície, visto que as linhas de campo de uma carga pontual são radiais. Por isso, pode-se concluir que se uma carga está fora de uma superfície, então o fluxo do campo elétrico dessa carga através da superfície é nulo, ou seja:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

$\Phi _{E}=\oint _{S}\mathbf {E} \cdot \mathrm {d} \mathbf {A} =0$ , se $�$ estiver externa à superfície.

As linhas de campo elétrico entram e saem da superfície, portanto o fluxo de campo elétrico sobre a superfície é nulo.

Lei de Gauss

A lei de Gauss estabelece uma relação entre o fluxo de campo elétrico através de uma superfície fechada e as cargas que estão no interior dessa superfície. Algumas considerações importantes sobre a de lei de Gauss são:

A lei de Gauss não contém nenhuma informação que não esteja contida na lei de Coulomb e no princípio da superposição. Inclusive, é possível obter a lei de Coulomb a partir da lei de Gauss e vice-versa.^[3]
É fundamental para a lei de Gauss, o fato de que a força elétrica é proporcional ao inverso do quadrado da distância. É esse fato que faz com que o fluxo de E não dependa da "superfície gaussiana" escolhida e dependa apenas das cargas que estão localizadas no interior da superfície. Dessa forma, é possível pensar numa lei de Gauss que estabeleça uma relação de fluxo para qualquer campo cuja lei de força associada a esse campo seja proporcional ao inverso do quadrado da distância, como a força gravitacional, por exemplo, logo existe uma lei de Gauss da gravitação.^[3]
Apesar da lei de Coulomb nos fornecer o necessário para calcular o campo elétrico de uma distribuição de cargas, muitas vezes, as integrais que envolvem o cálculo do campo elétrico podem ser complicadas de serem resolvidas, mesmo para casos razoavelmente simples. É nesse ponto que reside um dos aspectos de maior eficiência da lei de Gauss: o cálculo do campo elétrico em distribuições de carga que possuam determinados tipos de simetria torna-se extremamente simples.^[3]
A lei de Gauss se refere sempre ao fluxo no interior de uma superfície gaussiana escolhida. Portanto, para utilizar a lei de Gauss, é necessário definir o que é uma "superfície gaussiana". Esta é, por sua vez, uma superfície arbitrariamente escolhida. Normalmente, essa superfície é escolhida de modo que a simetria da distribuição de carga permita, ao menos em parte da superfície, um campo elétrico de intensidade constante.^[2]

Forma integral da lei de Gauss

Superfície gaussiana esférica centrada em q.

Para entender como a lei de Gauss relaciona o fluxo do campo elétrico no interior de uma superfície gaussiana com a carga no interior dessa mesma superfície, escolhe-se uma superfície qualquer com uma carga q em seu interior. Então, escolhe-se outra superfície gaussiana S' que está envolvendo q no interior de S. A forma dessa superfície S' pode ser qualquer, contudo, a fim de facilitar os cálculos e a visualização, vamos fazer dessa superfície S', uma esfera de raio r centrada na carga q. O raio r é tal que S' esteja inteiramente dentro de S.^[4] O fluxo do campo elétrico através dessa esfera é dado por:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\Phi _{E}=\oint _{S'}\mathbf {E} \cdot \mathrm {d} \mathbf {A}

Como tanto E quanto dA são radiais, o produto escalar torna-se o produto dos módulos, então:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\Phi _{E}=\oint _{S'}E\ dA

Como |E| é constante na superfície da esfera, podemos tirá-lo da integral e temos:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\Phi _{E}=E\oint _{S'}dA=\left({\frac {1}{4\pi \varepsilon _{0}}}{\frac {q}{r^{2}}}\right)(4\pi r^{2})={\frac {q}{\varepsilon _{0}}}

Portanto, é possível observar que o fluxo através da superfície S' é um número que independe do raio da esfera. Dessa forma, o fluxo que sai da superfície S também será ${\frac {q}{\varepsilon _{0}}}$ . Esse é um valor independente da forma da superfície S, desde que esta tenha uma carga q em seu interior. Se uma carga q está no exterior da superfície S, as suas linhas de campo entram e saem da superfície S, por isso, o fluxo de campo elétrico dessa carga sobre a superfície é nulo. Logo:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\oint _{S}\mathbf {E} \cdot \mathrm {d} \mathbf {A} =0{\text{, se a carga está no exterior da superfície gaussiana.}}

Por fim, se tivermos mais de uma carga no interior da superfície gaussiana, vale o princípio da superposição de modo que:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\oint _{S}\left(\mathbf {E_{1}} +\mathbf {E_{2}} \right)\cdot \mathrm {d} \mathbf {A} =\oint _{S}\mathbf {E_{1}} \cdot \mathrm {d} \mathbf {A} +\oint _{S}\mathbf {E_{2}} \cdot \mathrm {d} \mathbf {A} ={\frac {q_{1}+q_{2}}{\varepsilon _{0}}}

Portanto, a Lei de Gauss na forma integral pode ser enunciada da seguinte forma:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\oint _{S}\mathbf {E} \cdot \mathrm {d} \mathbf {A} ={\frac {q_{int}}{\varepsilon _{0}}}

Forma diferencial da lei de Gauss

[Expandir]Demonstração

Relação entre a lei de Gauss e a lei de Coulomb

[Expandir]Demonstração

Aplicações

É importante ressaltar que a lei de Gauss se torna eficiente apenas em casos em que há simetria. Mais precisamente, nos casos nos quais existe simetria esférica, cilíndrica ou plana.^[3] Dessa forma, construir superfícies gaussianas que aproveitem a simetria é de vital importância para a aplicação da lei de Gauss,^[2] visto que a eficiência da lei de Gauss consiste em utilizar a simetria das distribuições de carga para calcular campo elétrico dessas com mais facilidade.^[2]^[3]

Campo elétrico no interior e no exterior de uma esfera

Duas superfícies gaussianas esféricas em torno de uma esfera uniformemente carregada de raio R. A superfície gaussiana externa à esfera de raio R possui raio r' e a superfície gaussiana interna à esfera possui raio r.

Para uma esfera de raio R com carga Q uniformemente distribuída pela esfera, tem-se:

No exterior da esfera

Para se obter o campo no exterior da esfera, escolhe-se, como superfície gaussiana, a superfície esférica de raio r', situada no exterior da esfera de raio R. Pode-se imaginar que, muito longe da esfera, o campo elétrico que se sente é como o campo de uma carga puntiforme. Além disso, devido à simetria esférica, o campo elétrico deve apontar na direção radial. Dessa forma, aplicando a lei de Gauss:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\oint _{S}\mathbf {E} \cdot \mathrm {d} \mathbf {A} ={\frac {q_{int}}{\varepsilon _{0}}}={\frac {Q}{\varepsilon _{0}}}

O campo deve apontar na direção radial e, portanto, E e dA possuem a mesma direção e sentido e, por isso, segue que: E . dA = E dA. Logo:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\oint _{S}E\ dA={\frac {Q}{\varepsilon _{0}}}

O módulo do campo elétrico na superfície gaussiana é constante, visto que, nesse caso, o campo deve depender da distância em relação à esfera e, portanto, E pode sair da Integral.

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

E\oint _{S}dA={\frac {Q}{\varepsilon _{0}}}

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

E\left(4\pi r'^{2}\right)={\frac {Q}{\varepsilon _{0}}}

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

E={\frac {1}{4\pi \varepsilon _{0}}}{\frac {Q}{r'^{2}}}

Logo:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\mathbf {E} ={\frac {1}{4\pi \varepsilon _{0}}}{\frac {Q}{r'^{2}}}{\hat {\mathbf {r} }}

No interior da esfera

Para como o campo elétrico varia no interior da esfera, deve-se tomar como superfície gaussiana a superfície esférica de raio r no interior da esfera de raio R. Nesse caso, como a carga está uniformemente distribuída pela esfera, a densidade volumétrica de carga, ρ, é a mesma em todos os pontos da esfera,então pode-se observar que:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

q_{int}=\rho V_{g}=\left({\frac {Q}{{\frac {4}{3}}\pi R^{3}}}\right)\left({\frac {4}{3}}\pi r^{3}\right)=Q\ {\frac {r^{3}}{R^{3}}}

onde V_g é o volume da superfície gaussiana escolhida.

Dessa forma:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\oint _{S}\mathbf {E} \cdot \mathrm {d} \mathbf {A} ={\frac {Q}{\varepsilon _{0}}}\ {\frac {r^{3}}{R^{3}}}

Os mesmos argumentos dados anteriormente para que o produto escalar E . dA seja E dA e para que E saia da integral continuam sendo válidos, logo:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\oint _{S}E\ dA={\frac {Q}{\varepsilon _{0}}}\ {\frac {r^{3}}{R^{3}}}

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

E\oint _{S}dA={\frac {Q}{\varepsilon _{0}}}\ {\frac {r^{3}}{R^{3}}}

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

E\left(4\pi r^{2}\right)={\frac {Q}{\varepsilon _{0}}}\ {\frac {r^{3}}{R^{3}}}

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

E={\frac {Q}{4\pi \varepsilon _{0}}}{\frac {r}{R^{3}}}

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

Logo:

\mathbf {E} ={\frac {Q}{4\pi \varepsilon _{0}}}{\frac {r}{R^{3}}}{\hat {\mathbf {r} }}

Portanto, no caso de uma esfera uniformemente carregada:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\mathbf {E} ={\begin{cases}{\frac {Q}{4\pi \varepsilon _{0}}}{\frac {r}{R^{3}}}{\hat {\mathbf {r} }},&{\mbox{se }}r<R\\{\frac {1}{4\pi \varepsilon _{0}}}{\frac {Q}{r^{2}}}{\hat {\mathbf {r} }},&{\mbox{se }}r>R\end{cases}}

Campo elétrico no interior e no exterior de uma casca esférica

Para se resolver esse problema, utiliza-se a figura 4 novamente, porém com uma ligeira diferença: o interior da esfera de raio R é "oco", isto é, tem-se apenas uma casca esférica com carga Q uniformemente distribuída sobre sua superfície.

No exterior da esfera

Escolhendo a superfície de raio r' como mostrada na figura 4, tem-se, pela lei de Gauss, o mesmo resultado que foi obtido para o campo no exterior de uma esfera. A carga interna à superfície gaussiana, q_int, é Q nesse caso, como no caso anterior da esfera uniformemente carregada, de forma que o cálculo para o campo elétrico exterior à da casca esférica se desenvolve da mesma forma que o cálculo para o campo no exterior à esfera uniformemente carregada, então:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\mathbf {E} ={\frac {1}{4\pi \varepsilon _{0}}}{\frac {Q}{r'^{2}}}{\hat {\mathbf {r} }}

No interior da casca esférica

Escolhendo a superfície gaussiana de raio r, no interior da casca esférica, tem-se:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\oint _{S}\mathbf {E} \cdot \mathrm {d} \mathbf {A} ={\frac {q_{int}}{\varepsilon _{0}}}=0

\oint _{S}E\ dA=0

E\oint _{S}dA=0

E\left(4\pi r^{2}\right)=0

Portanto:

E=0

Logo:

\mathbf {E} =\mathbf {0}

Portanto, no caso de uma casca esférica uniformemente carregada:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\mathbf {E} ={\begin{cases}\mathbf {0} ,&{\mbox{se }}r<R\\{\frac {1}{4\pi \varepsilon _{0}}}{\frac {Q}{r^{2}}}{\hat {\mathbf {r} }},&{\mbox{se }}r>R\end{cases}}

Campo elétrico de um plano infinito

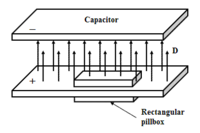
Figura 5: Um exemplo de superfície gaussiana que se deve utilizar para obter o campo de um plano infinito é como a que está mostrada sobre a placa de baixo do capacitor.

Supõe-se um plano infinito com densidade de carga σ e se deseja calcular o campo elétrico produzido por esse plano. Apesar de o problema ser bem diferente do apresentado na figura 5, visto que, no problema em questão, está-se estudando um plano infinito e não o campo no interior de um capacitor, é interessante utilizar uma superfície gaussiana de mesma forma que a superfície retratada na placa de baixo do capacitor da figura 5. Utilizando, portanto, a superfície de um paralelepípedo cortando o plano infinito como superfície S, tem-se:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\oint _{S}\mathbf {E} \cdot \mathrm {d} \mathbf {A} ={\frac {q_{int}}{\varepsilon _{0}}}

Por simetria, o campo elétrico deve apontar para "fora" do plano, isto é, ele aponta na direção ${\hat {\mathbf {z} }}$ para pontos acima do plano e na direção $-{\hat {\mathbf {z} }}$ para pontos abaixo do plano. Dessa forma, as únicas superfícies superior e inferior da superfície do paralelepípedo é que serão "furadas" pelo campo elétrico, por isso:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\oint _{S}\mathbf {E} \cdot \mathrm {d} \mathbf {A} =\int _{S1+S2}\mathbf {E} \cdot \mathrm {d} \mathbf {A} =\int _{S1+S2}E\ dA=E\int _{S1+S2}dA=2AE

onde A é a área da superfície superior e inferior da superfície do paralelepípedo. Sabe-se, também, que : σ = qint/A, logo : qint = σA, portanto:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

2AE={\frac {\sigma A}{\varepsilon _{0}}}

E={\frac {\sigma }{2\varepsilon _{0}}}

\mathbf {E} ={\frac {\sigma }{2\varepsilon _{0}}}{\hat {\mathbf {n} }}

onde ${\hat {\mathbf {n} }}$ é um vetor unitário que aponta para fora da superfície do plano.

Figura 6: Superfície gaussiana cilíndrica envolvendo um fio extenso positivamente carregado.

Campo elétrico de uma carga uniformemente distribuída ao longo de um fio extenso

Vamos considerar um fio longo que possui uma densidade linear uniforme de cargas $\lambda$ positiva em toda sua extensão. Podemos determinar o campo elétrico produzido por esta distribuição de cargas através da Lei de Gauss. Para tal, devido à simetria cilíndrica existente, vamos escolher como superfície gaussiana uma superfície cilíndrica de raio $�$ e comprimento $ℎ$ , coaxial com o fio, como mostrado na Figura 6. Como o fio possui uma densidade linear de cargas uniforme, podemos relacionar a carga contida no interior da superfície gaussiana com esta densidade pela seguinte expressão: $q_{int}=\lambda h$ . Dessa forma, a Lei de Gauss pode ser escrita como^[2]:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\oint _{S}\mathbf {E} \cdot d\mathbf {A} ={\dfrac {q_{int}}{\varepsilon _{0}}}={\dfrac {\lambda h}{\varepsilon _{0}}}

Uma vez que o fio está carregado positivamente e considerando sua simetria cilíndrica, esperamos que o campo elétrico produzido por ele aponte radialmente para fora do fio. Tal característica faz com que o fluxo de campo elétrico seja nulo nos planos da base da superfície gaussiana, isto é, $\mathbf {E} \cdot d\mathbf {A} =0$ , já que o ângulo entre ${\textbf {E}}$ e $d\mathbf {A}$ é $90^{\circ }$ . Na superfície lateral, o diferencial de fluxo passa a ser escrito como $� � �$ , já que o ângulo entre ${\textbf {E}}$ e $d\mathbf {A}$ é $0^{\circ }$ . Dessa forma, sendo $2\pi rh$ a área lateral da superfície gaussiana, temos que (onde SL significa Superfície Lateral):

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

E\int _{SL}dA={\dfrac {\lambda h}{\varepsilon _{0}}}

E\cdot (2\pi rh)={\dfrac {\lambda h}{\varepsilon _{0}}}

E={\dfrac {1}{2\pi \varepsilon _{0}}}{\dfrac {\lambda }{r}}

Logo, a expressão vetorial da distribuição espacial do campo elétrico resulta em:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\mathbf {E} ={\dfrac {1}{2\pi \varepsilon _{0}}}{\dfrac {\lambda }{r}}\mathbf {\hat {r}}

Lei de Gauss para dielétricos

Figura 7: Ilustração da polarização de um material dielétrico.

Cargas livres e cargas ligadas

Ver artigo principal: polarização dielétrica

Um dielétrico em presença de um campo elétrico, sofre o que se chama de polarização. A polarização consiste na separação das cargas positivas e negativas desse dielétrico, visto que o campo elétrico acelera cargas positivas no sentido do campo e cargas negativas no sentido oposto. Essas cargas geradas por esse efeito de polarização é o que se chama de cargas ligadas. O material passa a ser constituído de dipolos, como mostrado na figura 6. Dessa forma, as cargas estão "presas" aos dipolos, não estão livres para se mover. Por sua vez, é chamado de carga livre, o restante das cargas, que não foram geradas por esse efeito de polarização. As cargas livres são as cargas com as quais se está mais habituado quando se estuda eletrostática.^[3] Desse modo, num dielétrico, a densidade volumétrica de carga pode ser escrita como:

$equação Graceli dimensional relativista tensorial quântica de campos$

$[$ $\psi ^{*}$ $\psi ^{*}$ $G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$ $-i\hbar {\frac {\partial }{\partial x_{n}}}$ $.$ = $\left|\psi ({\vec {r}},t)\right\rangle$ /

$G_{\mu \nu }\$ $T_{\mu \nu }$ G $T^{\nu }{}_{\alpha }$

$\psi ^{*}$

//////

\rho =\rho _{lig}+\rho _{liv}

onde $\rho _{lig}$ é a densidade volumétrica de carga ligada e $\rho _{liv}$ é a densidade volumétrica de carga livre.

Pesquisar este blog

MECÂNICA GRACELI GENER. - QUÂNTICA DIMENSIONAL TENSORIAL RELATIVISTA DE CAMPOS [714]

História

Lei de Faraday-Neumann-Lenz

Enunciado qualitativo

Enunciado quantitativo

Equação de Maxwell-Faraday

Fluxo do campo elétrico

Lei de Gauss

Forma integral da lei de Gauss

Forma diferencial da lei de Gauss

Relação entre a lei de Gauss e a lei de Coulomb

Aplicações

Campo elétrico no interior e no exterior de uma esfera

Campo elétrico no interior e no exterior de uma casca esférica

Campo elétrico de um plano infinito

Campo elétrico de uma carga uniformemente distribuída ao longo de um fio extenso

Lei de Gauss para dielétricos

Cargas livres e cargas ligadas

Comentários

Postar um comentário

Postagens mais visitadas deste blog